機械学習（二値分類問題を考えます）において不均衡なデータセット（クラス間でサンプルサイズが大きく異なる）を扱う場合、多数派のクラスのサンプルに対してサンプリング行い均衡なデータセットに変換するダウンサンプリングが良く行われます。

この不均衡データのダウンサンプリングによって、サンプル選択バイアスが生じることが Calibrating Probability with Undersampling for Unbalanced Classification という論文で説明されています。

具体的には、少数派クラスの事前確率が大きくなります。一般的な問題設定では、正例のクラスが少数派クラスであるので、正例と予測される確率（事後確率）が大きくなります。

予測確率が重要な場合 *1 は特に、このバイアスの影響を除去しなければなりません。

実際、FacebookのCTR予測に関する論文でも、このバイアスの影響を除去するために予測確率に対するcalibrationを行っていることが記載されています。

バイアスの影響と予測確率のcalibration
実験
まとめ

バイアスの影響と予測確率のcalibration

知りたいのは、ダウンサンプリングを行ったデータセットで学習されたモデルの予測確率と、元の不均衡なデータセットで学習されたモデルの予測確率の間の関係です。

ここで、クラス0を負例、クラス1を正例とする二値分類を考えます。正例の数 << 負例の数であり、ダウンサンプリングが行われたとします。

$(\mathcal{X}, \mathcal{Y})$ を元の不均衡なデータセット、 $(X, Y)$ をダウンサンプリング後の均衡なデータセットとします。つまり $(X, Y) \in (\mathcal{X}, \mathcal{Y})$ です。元の不均衡なデータセットにおけるサンプル $(x, y) \in (\mathcal{X}, \mathcal{Y})$ が、ダウンサンプリング後のデータセット $(X, Y)$ に含まれていれば 1、そうでなければ 0 を取るバイナリの確率変数 $s$ を導入します。

確率変数 $s$ を用いると、ダウンサンプリングを行ったデータセットで学習されたモデルの予測確率は $p(y = 1 | x, s=1)$ と表現できます。これを $p_s$ とおきます。一方、元の不均衡なデータセットで学習されたモデルの予測確率は $p(y = 1 | x)$ と表現できます。これを $p$ とおきます。

詳細は省きますが、Calibrating Probability with Undersampling for Unbalanced Classification に記載されているとおり、 $p_s$ と $p$ は以下の関係式で表現できます。

$p_s = \frac{p}{p + \beta (1 - p)}$

ここで、 $\beta = p(s=1 | y = 0)$ です。これはダウンサンプリング率を表現しています。

式変形を行うことで、以下の式を導くことができます。

$p = \frac{p_s}{p_s + \frac{(1 - p_s)}{\beta}}$

つまり、ダウンサンプリングを行ったデータセットで学習されたモデルの予測確率 $p_s$ に対して、ダウンサンプリング率 $\beta$ を用いて上式でcalibrationを行うことで、バイアスの影響を除去できることになります。

実験

実際に不均衡データに対して、バイアスの影響とcalibrationの効果を確認してみます。まずは、scikit-learnのmake_classificationを使用して、正例:負例 = 1:9でサンプル生成します。また、学習データとテストデータに分割します。

from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
# 正例:負例 = 1:9でサンプル生成
X, y = make_classification(n_samples=100000,
                           n_features=5,
                           n_classes=2,
                           weights=[0.9, 0.1],
                           random_state=42)
# 学習・テストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X,
                                                    y,
                                                    test_size=0.2,
                                                    random_state=0)

次にimbalanced-learnを用いて、正例:負例 = 1:1になるように学習データの負例に対してダウンサンプリングを行います。

from imblearn.under_sampling import RandomUnderSampler
sampler = RandomUnderSampler(sampling_strategy={0: y_train.sum(), 1: y_train.sum()}, random_state=42)
X_train_sampled, y_train_sampled = sampler.fit_sample(X_train, y_train)

そして、ダウンサンプリングを行ったデータセットを用いてロジスティック回帰の分類器を学習して、テストデータに対して予測を行います。

from sklearn.linear_model import LogisticRegression
model = LogisticRegression(random_state=42, solver='lbfgs')
model.fit(X_train_sampled, y_train_sampled)
y_proba = model.predict_proba(X_test)

ここで、予測確率のヒストグラムを可視化してみます。紫の線はテストデータにおける正例の割合、緑の線はテストデータに対する予測確率の平均を表しています。その2つの値に大きな乖離があることが分かります。

f:id:pompom168:20190721235051p:plain

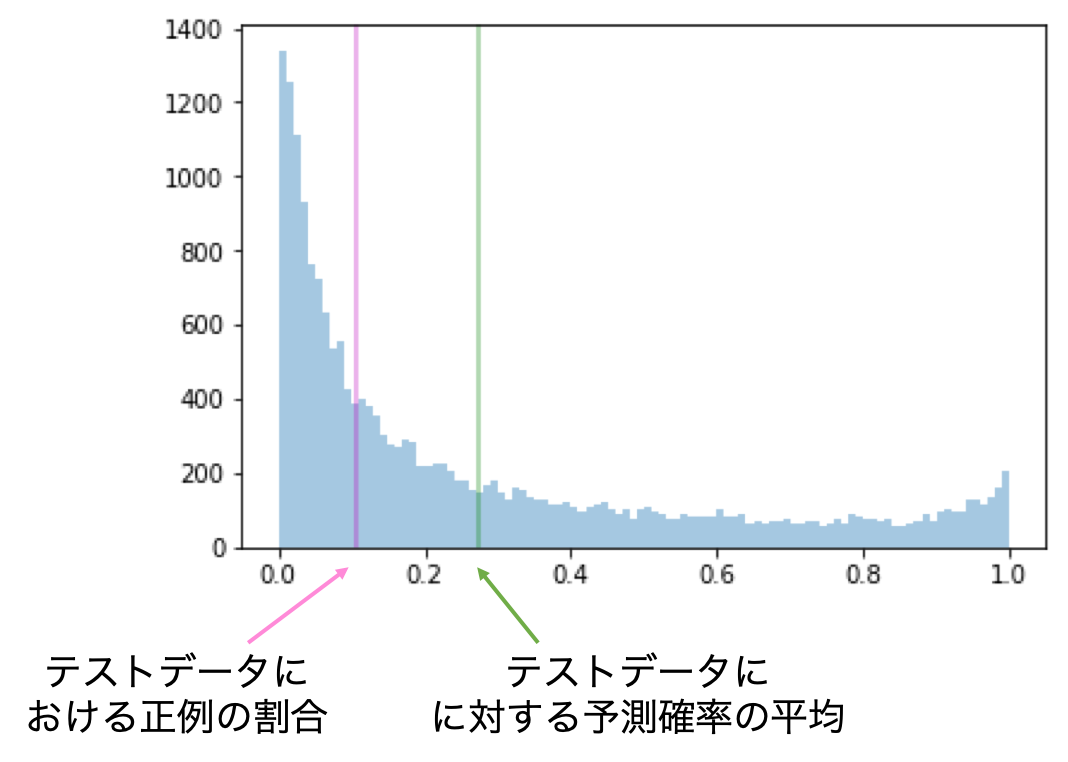
次に、テストデータの予測確率に対してcalibrationを行います。

def calibration(y_proba, beta):
    return y_proba / (y_proba + (1 - y_proba) / beta)

sampling_rate = y_train.sum() / len(y_train)
y_proba_calib = calibration(y_proba[:, 1], sampling_rate)

calibration後の予測確率に対して、上と同様にヒストグラムを可視化してみます。紫と緑の線がかなり近づいており、現実に即した予測確率になっていると言えそうです。

f:id:pompom168:20190721235103p:plain